Graph of wavefunction for a particle in a 2D box where \( n_x \) and \(n_y \) are equal to 2
Graph of the square of the wavefunction
Thanks to CrazyPenguin0111, for the hard work in researching and writing the information below.
There are two main quantum mechanical phenomena that inspired Entanglement Chess, superposition and entanglement.
This section will go over both of these phenomena and try to explain them.
Please keep in mind that if you want to dive deeper into quantum mechanics this is not the place.
Some resources will be listed below if you want to learn more.
This section will only take a cursory look into both topics and won't go into the math behind the topics too much.
There might be some equations here and there but nothing serious.
While experience in higher level maths will help you understand some of these equations it is not necessary and the meaning of each equation will be explained as clearly as possible.
Whith all that in mind, lets take a look at these two topics.
Ok before we talk about superposition and entanglement we should first cover some basic information about quantum mechanics and some vocabulary as these terms will come up later.
FIrst off we should talk about what quatum mechanics is.
Quantum emechanics is the field of science that looks at how small particles interact with each other.
In quantum mechanics, various things about a particle can be found by using something called a wavefunction.
The wavefunction usually uses a Ψ or a Φ to symbolize it in equations.
The wavefuction is a function that relates the position (x,y,z) or (r,θ,φ) and time with a value.
For a function to be considered a valid wavefunction there are several traits it must have, such as being differentialable and have a value of zero at the boundaries.
The wavefunction should also be normalized meaning that the sum of the prbability of the particle everywhere inside the boundary should add up to 1.
The value of the wavefunction at a given point has no physical meaning.
However, the absolute square of the wavefucntion represents the probability distripution of a particle being in a certain location at a certain time.
The absolute square of the wavefuction can be found using the equation below.
\[ {\left| Ψ \right|}^2 = Ψ Ψ^* \]
where Ψ* is the complex conjugate of the wavefunction.
If the absolute square of the wavefunction represents the probability density of finding the particle at a certain psoiton, we should be able to do some math to calculate the probability of a particle being in a certain area.
To calculate the probability of finding a particle in a region we use the following equation
\[ P = \int_{τ_1}^{τ_2} \left| Ψ \right|^2 \, dτ = \int_{τ_1}^{τ_2} Ψ Ψ^* \,dτ \]
In this equation we are integrating over two points in a space, τ_1 and τ_2. Over some differential dτ. We are using τ here as a generalized coordinate. τ could be some x,y,z corrdinate or any other valid coordinate system.
If you don't know what integrals are its fine, you can think of integrals as adding the output value of a function over some region.
In this case its like adding the probability of finding a particle over a certain region. If you add up the probabilities of the entire region the total probability equals 1.
If we are integrating ovver the entire region we can use a shrothand way of writing out the integral using dirac noation.
Dirac notaion is very useful in quantum mechanics as it allows us to shorten very long equations into just a few symbols so its easier to read and understand.
I will quickly go over dirac notation on a cursory level because it is used later.
As I said eariler if we intergrate over the whole region we can use dirac notaion which is shown below.
\[ \int_{τ} \left| Ψ \right| ^2 \, dτ = \int_{τ} Ψ^* Ψ\, dτ = ⟨ψ|ψ⟩ = 1 \]
Dirac notaion has two main operators.
The bra, ⟨ψ|, and the ket, |ψ⟩, together they make a braket.
Putting a wavefunction inside a bra turns it into its complex conjugate \( ⟨ψ| = Ψ^* \)
bras and kets can also be thouhgt as vectors.
A bra is defined as \( ⟨A| = \begin{pmatrix} {A_1}^* & {A_2}^* & {A_3}^* & ... & {A_n}^* \\ \end{pmatrix} \)
A ket is defined as \( |B⟩ = \begin{pmatrix} B_1 \\ B_2 \\ B_3 \\ . \\ .\\ . \\ B_n \\ \end{pmatrix} \)
If a bra and a ket are multiplied together in that order it is considered the inner or dot product.
If the ket and the bra are multiplied together in that order it considered the outer or cross product.
Multiplying bras and kets are similar to matrix multiplication.
If you do not know how to multiply matrices, its fine because we don't need it later in this page.
Now that we covered some of the math behind quantum mechanics we can start using that math to find physical quantities.
We can find these physical quantities by using the wave funtion and applying operators on them.
Operators are things that take in a function and output another function.
In quantum mechanics, there is always some uncertainty in measurements no matter how accurate and precise the the instrument is.
Therefore, when scientists talk about quantities in quantum mechanics they usually refer to the average value of the quantity otherwise known as the expected value.
The expected value can be found using the following formula.
\[ ⟨ω⟩ = ⟨Ψ | \hatΩ |Ψ⟩ \]
Where \( \hatΩ \) is a quantum operator and \(⟨ω⟩\) is the expected value of the physical quantity, ie position, momentum and energy.
Now that we covered the basics we can finally start talking about superposition.
Superposition is where a particle or an object that follows the laws of quantum mechanics is in multiple classical states at the same time.
A common example of superposition is Schroedinger's Cat.
Schroedinger's Cat is a thought experiement created by Erwin Schroedinger, where a cat is placed in a box.
Also in the box is an atom of a radioactive isotope that has a 50% chance of decaying in the next minute, a device that can detect if the atom decayed or not, and a device that will smash a vial of poison when it recieves a signal from the detector.
If you leave the cat in the box for a minute and come back to open it after a minute has passed there are two possibilities that can happen, the cat is still alive or the cat is dead.
In the moment before you open the box the cat is in a superposition state of alive AND dead at the same time.
When you open the box to see if the cat is alive or dead the superposition collapses into a classical state of alive OR dead.
Often times scientists who study quantum mechanics need to solve equations reguarding particles in superpositions states so it is more convenient to write superposition states in the form of a mathematical expression.
We can write the superposition of the cat being alive and dead as follows.
\[ \sum_{i=1} \left| {c_i} \right|^2 = ⟨ψ|ψ⟩ = 1 \] In this case of Schroedinger's Cat, because the cat has a 50% chance of being alive and a 50% chance of being dead \( c_1 = c_2 = {\sqrt{2} \over 2} \).
At the start of the game in Entanglement Chess all the pieces are also in a superposition that can be represented by the following expression.
\[ {\sqrt{6} \over 6} |Pawn⟩ + {\sqrt{6} \over 6} |Knight⟩ + {\sqrt{6} \over 6} |Rook⟩ + {\sqrt{6} \over 6} |Bishop⟩ + {\sqrt{6} \over 6} |Queen⟩ + {\sqrt{6} \over 6} |King⟩ \] A more realistic example of superposition can be seen for a particle in a 2 dimensional box.
Assuming that the particle cannot leave the box, the position of the particle must be somewhere in the box.
Therefore, the particle is in a superposition state reguarding its position.
The possible positions are defined by x=[0,Lx] and y=[0,Ly], where Lx and Ly are the length of the box in the x and y direction.
This is what's called the boundary condition and using this we can derive a wave function that describes the particle we are looking at.
We won't go into deriving wavefunctions here but there will be resources to do so in the resources section.
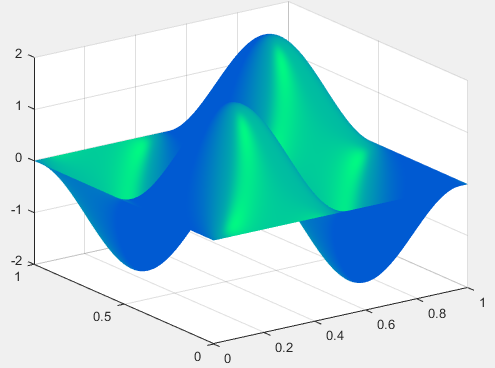
In any case the equation for the wavefunction for a particle in a 2 dimensional box is shown below as well as its graph.
Graph of wavefunction for a particle in a 2D box where \( n_x \) and \(n_y \) are equal to 2
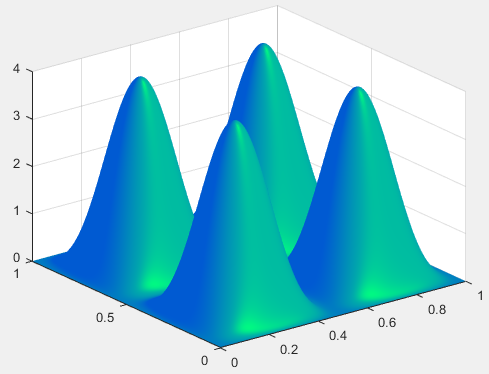
Graph of the square of the wavefunction
The graphs above show what the wavefunction looks like in an unobserved state.
Because the particle's position was not measured, the wavefunction has a non zero value everywhere in the interior of the box and has a value of zero on the edges and corners of the box.
We can say that the particle is in a superposition of various positions with varying probability amplitudes.
However, if the position of the particle has been measured the wavefunction undergoes a process called wavefunction collapse.
This causes the particle to not be in superposition and pick a single classical state to occupy.
For this example, that means the particle will pick a random location somewhere inside the box based on the probabilities of it being at that spot, which can be seen in the square of the wavefunction graph.
The subsequent probability distribution of the particles is shown below.
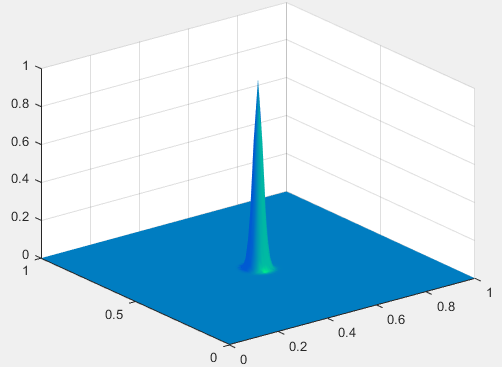
Graph of collapsed wavefunction
As you can see the wavfunction became a single peak at a specific location. Instead of the probability wave being spread out over the area of the box.
Quantum entanglement is the phenomenon where the state of particles cannot be described independently.
This occurs when particles are created near each other or interact in specific ways.
An example of entanglement is when two electrons share a common atomic orbital.
Two electrons in the orbital cannot be described independently and the combined wavefunction of the orbital is not the product of the two wavefunctions of the individual electrons.
Furthermore, if the spin of one electron is measured, the other electron will have the opposite spin.
This is a result of the electrons in the orbitals being fermions, and since two fermions cannot be in the same state at the same time the two electrons are forced to have opposite spins.
Fermions are a type of particle with half integer spin values. All matter particles like the elctron, mueon, quarks, etc... are fermions.
Whereas all the force carrying particles like the photon, the W and Z Boson, Gluons and the Higgs Boson are all bosons, which have a whole integer spin value.
Just to clarify, fundemental particles don't physically spin, spin is just a property of a particle that contributes to the angular momentum of the system.
Entanglement can also be seen in Entanglement Chess, who knew right?
At the start of the game all the pieces are entangled with each other.
However, when the identity of one piece is found, lets say the king for example, it puts a restriction on what the other pieces can be.
In the case of the king because a player can only have one king during the game we can automatically rule out the fact that the other pieces can be kings.
The same logic can be used to rule out possible identities for other pieces as well.
I hope you enjoyed reading my page on the quantum mechanics of entanglement chess and I hope you learned a bit about quantum mechanics.
Writing my first webpage with no prior experience or knowledge was an interesting experience.
As a concluding note I hope that you have fun playing quantum chess while now knowing about the principles that inspired it.
- CrazyPenguin0111